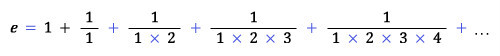| 자연상수 e, 원주율 π는 무리수라는데 왜 그럴까? 그리고 자연상수 e, 원주율 π는 또 초월수라고 하는데 초월수라는 것은 무엇일까? |
|
자연상수 e는 어떤 수인가?

곡선 y=1/x 와 x축, x=1, x=a 로 둘러싸인 영역의 넓이가 1이 되는 수 a > 1를 자연상수 e라고 정의한다. 그 외에도 e를 정의하는 방법은 여러 가지가 있다. e는 수학 및 공학 등에 없어서는 안 될 중요한 자연계의 기본 상수이다. |
|
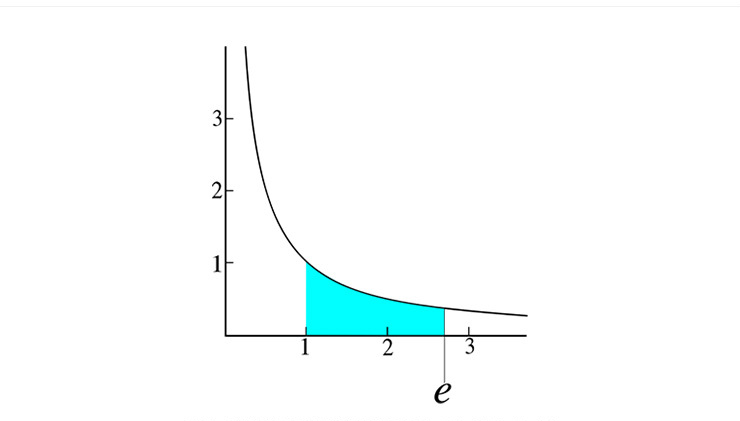
곡선은 y=1/x의 그래프, 파란색 부분의 면적이 1 <출처: Cronholm144 at wikipedia>

자연상수 e는 오일러가 무리수라는 것을 증명했다

e의 근삿값은 2.718281828459…로 알려져 있다. 근삿값 2718281828459/1000000000000를 연분수로 써 보면, 정수부분이 2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 13 …임을 계산할 수 있다. 끝부분에서 조금 빗나갔지만, 더 정밀한 근삿값을 써서 계산하면 e의 연분수 전개에 어떤 규칙성이 있는지 확연해진다. 실제로 영국 수학자 로저 코츠(Roger Cotes, 1682-1716)는 이런 계산을 통해 다음을 발견했지만 엄밀한 증명은 내놓지 못했다. 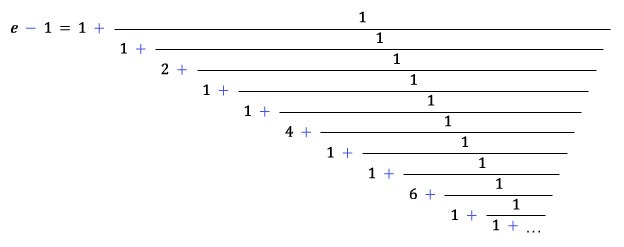
1737년 오일러(Euler, 1707-1783)가 만족할만한 증명을 하여 e가 무리수라는 것을 최초로 증명한 사람이 됐다. 이 증명은 다소 복잡한 수열의 일반항을 구하는 문제와 미분방정식 문제가 엮여 있어 비수학자들에게는 다소 어려운 편이다. 요즘은 보통 푸리에(Joseph Fourier, 1768-1830)의 방법을 따라 아래와 같은 사실을 이용하여 e가 무리수임을 증명하는데, 비교적 많이 알려져 있는 증명이므로 독자 중에 누군가는 증명을 써 줄 것으로 믿는다.
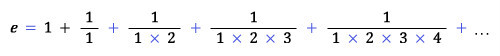
|
|
원주율π도 무리수라는 것은 람베르트가 증명했다

수학에서 가장 중요한 상수를 꼽으라면, 원주율 π를 빼 놓을 수 없다. π가 무리수라는 것은 스위스 수학자 람베르트(Johann Heinrich Lambert, 1728-1777)가 1761년 역탄젠트 함수의 연분수 전개를 이용하여 증명했다. 그 중 특수한 경우인 π의 연분수 전개가 아래처럼 제멋대로인 것을 보면, 기나긴 세월이 걸려서야 원주율이 무리수임을 증명한 것도 무리는 아니라는 생각이 든다. 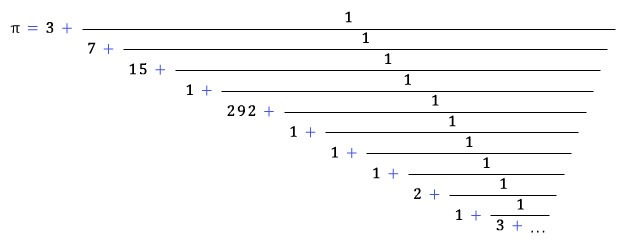
|
|
원주율π의 훌륭한 근삿값을 제시한 조충지


조충지(祖沖之, 429~500)
π의 연분수에서 2단계 근삿값은 3 + 1/7 = 22/7이다. 고대부터 원주율의 근삿값으로 22/7이 애용됐는데 최적의 근삿값이라는 것과 무관치는 않을 것이다.
3단계 근삿값은 333/106=3.141509…인데 16세기 유럽에서 사용한 근삿값으로, 흔히 사용하는 근삿값 3.14=314/100과 분모가 별 차이가 나지 않는데도 참값과의 오차는 훨씬 작다.
4단계 근삿값은 355/113=3.1415929…인데 이 값은 중국의 조충지(祖沖之, 429-500)가 유럽보다 1,000년 가량 앞서 발견한 것으로, 우연히도 최적의 근삿값을 얻은 것인지 놀랍기까지 하다. 이 근삿값은 소수점 6자리까지 정확하다.
π의 연분수에서 2단계 근삿값은 3 + 1/7 = 22/7이다. 고대부터 원주율의 근삿값으로 22/7이 애용됐는데 최적의 근삿값이라는 것과 무관치는 않을 것이다.
3단계 근삿값은 333/106=3.141509…인데 16세기 유럽에서 사용한 근삿값으로, 흔히 사용하는 근삿값 3.14=314/100과 분모가 별 차이가 나지 않는데도 참값과의 오차는 훨씬 작다.
4단계 근삿값은 355/113=3.1415929…인데 이 값은 중국의 조충지(祖沖之, 429-500)가 유럽보다 1,000년 가량 앞서 발견한 것으로, 우연히도 최적의 근삿값을 얻은 것인지 놀랍기까지 하다. 이 근삿값은 소수점 6자리까지 정확하다.
의 연분수에서 2단계 근삿값은 3 + 1/7 = 22/7이다. 고대부터 원주율의 근삿값으로 22/7이 애용됐는데 최적의 근삿값이라는 것과 무관치는 않을 것이다.
3단계 근삿값은 333/106=3.141509…인데 16세기 유럽에서 사용한 근삿값으로, 흔히 사용하는 근삿값 3.14=314/100과 분모가 별 차이가 나지 않는데도 참값과의 오차는 훨씬 작다.
4단계 근삿값은 355/113=3.1415929…인데 이 값은 중국의 조충지(祖沖之, 429-500)가 유럽보다 1,000년 가량 앞서 발견한 것으로, 우연히도 최적의 근삿값을 얻은 것인지 놀랍기까지 하다. 이 근삿값은 소수점 6자리까지 정확하다.
초월수는 정수 계수 다항식의 근이 아닌수

칸토르(Georg Cantor, 1845~1918)

e와 원주율π는 초월수이다

1873년 프랑스 수학자 에르미트(Charles Hermite, 1822-1901)가 e가 초월수임을 증명함으로써, 대수 방정식을 통해 e를 정의하려는 노력은 종지부를 찍게 됐다. 또한 1882년 독일 수학자 린데만(Ferdinand von Lindemann, 1852-1939)이 에르미트의 방법을 따라 π 역시 초월수임을 증명했다. 이로써 고대부터 내려오던 3대 작도 문제 중 하나인 ‘원과 같은 넓이의 정사각형을 자와 컴퍼스로 작도하기’가 불가능함도 증명됐다. 오늘날에는 부분적분법 및 고계도함수 등에 대한 약간의 지식만 있으면, e와 π가 초월수라는 것을 각각 A4 용지 두 장 정도에 증명할 수 있고, 무리수라는 것은 한 장 정도에도 증명할 수 있지만, 여백도 모자랄 뿐만 아니라 스크롤 내리는 소리가 들리는 듯하니 소개하지 않기로 한다. |
|
힐베르트의 7 번째 문제

다비트 힐베르트(David Hilbert, 1862-1943)가 제시한 20세기 수학이 해결해야 할 23개 문제 중에서 7 번째 문제는 크게 두 가지인데, 그 중의 하나는 다음과 같다. |
|


힐베르트(David Hilbert, 1862~1943)

못다한 이야기

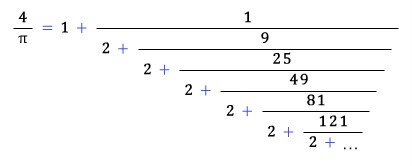
유리수냐 무리수냐 혹은 더 나아가서 초월수냐 그것이 문제인 수는 대단히 많다. 예를 들어, π+e, πe, π×e 와 같은 수를 비롯해, 제타함수의 홀수에서의 값인 ζ(5), ζ(7), ζ(9), … 등은 모두 (칸토르 덕에) 초월수로 짐작하지만 현재까지는 유리수냐 아니냐는 것조차도 알지 못한다. 간신히 ζ(3)은 무리수라는 것을 증명한 정도이고, 몇 가지 사실은 알려져 있다. 유리수냐 무리수냐를 모르는 대표적인 상수로 오일러-마스케로니 상수 γ라는 것이 있다. 아마 비수학자들에게는 생소할 듯 하나, 수학에서는 중요한 상수이다. 이 상수가 무리수라는 증명하는 것이 얼마나 어려웠던지, 유명한 수학자 하디(G. H. Hardy, 1877-1947)가 이렇게 말한 적이 있다. “γ가 무리수임을 증명한 사람에게 자신의 옥스퍼드 대학 서빌리언 석좌교수직을 양보하겠다.” 못다한 얘기는 많으나, 머리도 식힐(?) 겸 단순연분수는 아니지만 π에 관련한 규칙적인 연분수 하나를 감상하는 것으로 마무리할까 한다. |
|
- 글 정경훈 / 서울대 기초교육원 강의교수
- 서울대학교 수학과에서 학사, 석사, 박사를 받고, 포항공대, 연세대, 위스콘신대, 서울대에서 박사후 과정을 밟았다. 현재 서울대 기초교육원 강의교수이다.
발행일 2009.06.09
이미지 TOPIC / corbis